初级和二级垂轴色差

当离轴物点的不同颜色的光线聚焦在像面上的不同高度就可以看到垂轴色差。实际上，这是放大率的色变量。蓝光和红光的差别就是初级垂轴色差，黄光与红光的差别就是二级垂轴色差。在上表 1可以找出初级和二级垂轴色差的定义。垂轴色差是像边缘色散的原因。轴上点没有垂轴色差，轴上色晕的原因是轴向色差。垂轴色差随着视场角的增大而更加明显，在广角光学系统(光学透镜)中它常常很严重。需要记住的是，垂轴色差与 f/#无关，只与不同波长的主光线在像面上的高度有关。

色球差

色球差是球差关于波长的函数变化。通常，一个消色差双胶合在蓝光会有未校正或负的球差，在红光会有过校正或正的球差。如图 6a所示，表示不同玻璃类型的横向光线像差： 对于相对较低的F数如f/4的双胶合，主光线的球差很小，自然会使红光和蓝光球差很小。为了只考察剩余色球差，对第一个表面添加非球面，其目的是消除中心 0.5876μm 的 d光的球差。

在这些例子中，使用一个消色差双胶合，可见三个f/4镜头的色球差类似。而f/10镜头的色球差明显改善。对于相同 BK7和 SF2材料，若考虑 f/4镜头光瞳的中心部分（即 f/10），可以看出像差更线性而且更小的球差与色球差。因此，大 F数的镜头的色球差更明显。

玻璃选择会影响色球差，然而对于用在轴上点的双胶合，下面使用模拟玻璃来展示色球差的变化。对于图 6b 的光线像差曲线图，其使用了模拟玻璃的 f/5 双胶合产生。为了只探讨色球差，双胶合的第一个面使用非球面来消除主光线的球差，并使它们的局部色散相互匹配以消除二级光谱。 模拟玻璃的阿贝数取V1=64.167 以及V2=33.848 （它们分别是BK7和 SF2的阿贝数）。

图 7给出色球差产生的原因。在一个消色差双胶合中，第一个面和最后一个面是未校正球差产生的原因。中间那个面是过校正球差产生的原因。虽然主光线的球差已经被校正，但是因为有色差，无法保证其他波长的球差也能被校正。

理论上来说，如果红光和蓝光的光程差减小，那么色球差就会减小。可以减小第一面和第三面的光焦度来达到这个目的， 即这减小了光线偏折程度 （但是其他情况下这是不可行的，例如需要引入三阶球差）。减小元件的厚度在某种程度上也会有一定的帮助。

 

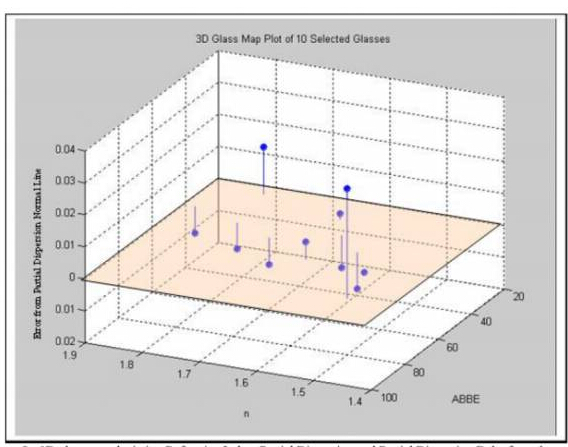
如图8所示，是一个三维图，其既包括传统的玻璃图也包括部分色散偏离正常直线的差值。这里的玻璃有 BK7，PSK53，KZFSN4，FK54和 SF6。这张表可以让我们同时找到折射率、阿贝数以及部分色散；可以让我们更快地选择合适的玻璃。

通过选择在同一个色散面上的两个玻璃，可以最小化二级色差，同时也要考虑阿贝数差别与折射率，这三个因素决定了玻璃的选择。注意，这里画出的是部分色散到正常直线的差值，相等的部分色散直线会被旋转，这个旋转量由玻璃 K7和F2所确定的直线的斜率决定。

为了助于玻璃选择以及熟悉常规玻璃的形式，把玻璃表分成 6个区域，如图 9所示。分区有助于理解整张玻璃表。这是很有用的，因为光学设计优化过程中通常需要让玻璃参数发生变化。优化玻璃参数通常会得到一个不实际的玻璃，这时候就需要设计者根据玻璃表来决定模拟玻璃所覆盖的范围。当这个范围结合优化函数，即 OPD 或横向光线像差，就有可能选出一个有益于整个设计的实际玻璃。

 

 

总结与结论

本文回顾了在光学系统中影响色差的一些因素。并分别叙述了每种典型色差。探讨了像差从何而来，以及如何消除它们。虽然现代光学设计通常是让程序“自动”选择玻璃。但是，很多时候是需要人为干涉的。 因此， 当优化光学系统时， 设计者应该要了解玻璃的详细特征。例如，消色差所选的玻璃是非环保难以制造以及透射性能不好，或者非常贵，那么最好选择另一个可替代的玻璃。通过了解，为何这个玻璃是首选玻璃，或者为何优化程序会选择这个玻璃，设计者就可以很有效地选择等效玻璃。双胶合实验表明，偏向高折射率的玻璃，且阿贝数差值在 20以上，以及接近的部分色散值，会得到一个较好的结果。