应用1：准直光束的聚焦

作为第一个案例，我们来看一个非常普遍的应用，把激光光束聚焦到一个很小的焦点上，如图一所示。我们有一束激光，光束半径为y1，发散角为θ1，它通过一个焦距为f的透镜聚焦。如图所示，我们有θ2= y1/f。光学不变量定律（y2θ2 = y1θ1）告诉我们，聚焦光斑的半径和发散角的乘积是个常量，因此可以得到y2= θ1f。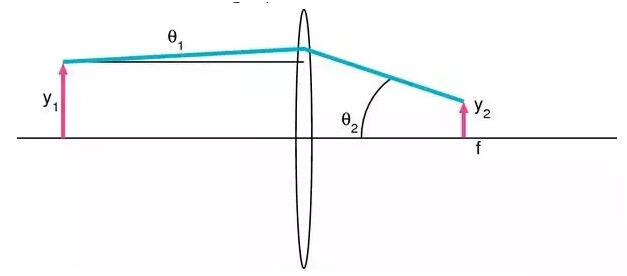

图一

让我们看一个具体的例子，使用一个LBK-5.9-10.3-ET1.9型号的平凸透镜对二氧化碳激光器的出射光束进行聚焦。假设二氧化碳激光器的光束直径为3 mm，全发散角为6 mrad。上述公式中的参数采用光束半径和半发散角，因此有y1= 1.5 mm 和 θ1 = 3 mrad。LBK-5.9-10.3-ET1.9的焦距为10.3 mm。因此，聚焦后焦点的半径为y2= θ1f =30.3 μm，也就是光斑直径为60.6μm。

我们假定使用了完美无相差的透镜。如需进一步减小焦点，我们必须使用短焦距的透镜或者首先对激光进行扩束。若这两种办法都受限于系统设计无法改变，那么60.6 μm就是我们可以实现的最小聚焦光斑。另外，光的衍射效应可能使实际的光斑更大一些，但在目前的讨论中我们不考虑波动光学的影响，只在几何光学的范畴中讨论。

应用2：点光源出射光的准直

另一个比较常见的应用是对从很小的一个光源发出的光进行准直，如图二所示。通常称这种光源为点光源。但是现实中没有绝对意义上的点光源，任何光源都有一定的尺寸，需要在计算中加以考虑。图二中的点光源半径为y1，最大发射角度为θ1。如果用一个焦距为f的透镜对出射光进行准直，那么得到的准直光束的半径为y2= θ1f，发散角为θ2 = y1/f。请注意，不论使用任何透镜，准直后的光束尺寸和发散角都成反比关系。例如，如果希望准直光的准直度增加两倍（θ2减小为1/2），那么光束的尺寸将相应地增加一倍。

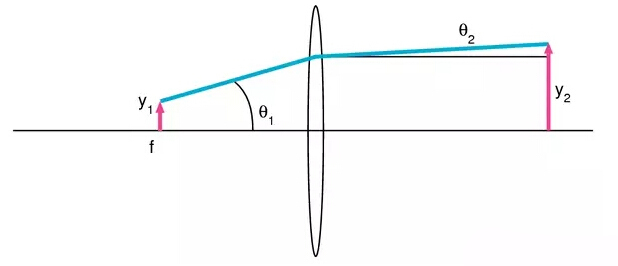
图二

现实中常见的一个应用是对光纤的出射光进行准直，我们以此作为具体案例加以讨论。某一光纤具有200 μm的芯径，数值孔径（NA）为0.37。因此光源半径y1=100μm。NA是用过光纤的出射角进行定义的，有θ1= 0.37。如果我们再一次使用焦距为10.3 mm的LBK-5.9-10.3-ET1.9透镜对出射光进行准直，准直后的光束半径将为3.8mm，发散角为9.7mrad。二者之间具有反比关系。如果希望得到更小的准直光束，那么必须接受更大的发散；相反如果希望在很长距离上保持光的准直度，我们必会得到更大的光束尺寸。

应用3：扩束

实际应用中经常需要对激光光束进行扩束。要实现这一功能，至少需要两片透镜。大多数激光扩束镜采用伽利略式设计，由正透镜和负透镜组合而成。由于较低的扩展系数，简单、紧凑的结构而被广泛应用，扩束镜通过放大激光光束来实现更小的聚焦光斑。

在图三中，一个半径为y1，发散角为θ1的光束经一个焦距为-f1的凹透镜达到扩束。根据应用1和2中的讨论我们知道，θ2= y1/|−f1|。光学不变量定律告诉我们，凹透镜产生的虚像大小为y2 = θ1|−f1|。这个像处于凹透镜的焦点位置。采用第二片焦距为f2的凸透镜，置于距离凹透镜f2-f1的位置处，对光进行准直，准直后的光束半径为y3= θ2f2，发散角为θ3 = y2/f2。

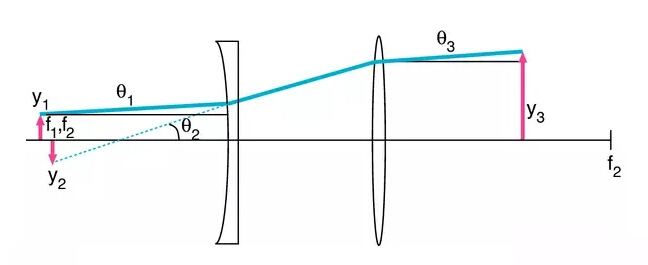
图三

这一系统的扩束系数定义为

y3/y1= θ2f2/θ2|−f1| = f2/f1

即两片透镜的焦距比。

比如，如果想要得到5倍的扩束效果，那么需要选择两片焦距相差5倍的透镜才可以实现，而扩束后的光束发散角也减小为原来的1/5。

为了使相差最小化，最好选择这种平凸和平凹透镜，并且使他们平面的一侧面对放置。使用透镜的中心部分可进一步减小相差，因此选择较大尺寸的透镜会有帮助。这种扩束的设计称为伽利略式扩束。采用两片正焦距的凸透镜同样可以实现扩束功能，称为开普勒式扩束，但这种设计的尺寸更长。南京波长的BEX系列扩束镜规格齐全，也可依据客户的需求进行定制，另外也有一些特性需求的扩束镜如高功率光束扩束器，主要应用于1030-1090nm光纤激光器，扩束镜采用的熔融石英材料以满足高功率应用，通过C接口连接。除了固定变倍扩束镜外，还有能覆盖从紫外到红外的变倍扩束镜，变倍范围可客样定制。

应用4：大尺寸光源的聚焦

这个应用类似于光学成像，而不同于上述讨论的准直和聚焦。一个典型的例子是把一个发射荧光的样品成像到CCD相机上，光路结构如图四所示。一个较大尺寸的光源，半径为y1，被放置于距离透镜s1的位置，透镜焦距为f，通光孔径为R。

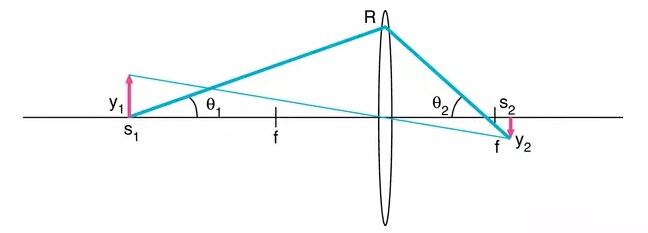
图四

如果s1比较大，那么s2将接近于透镜的焦点处f。因此，近似可得θ2~ R/f。然后根据光学不变量定律，可以得到y2= y1θ1/θ2 = y1(R/s1)(f/R)或者y2= 2y1(R/s1)(f/#)

其中f/#= f/2R= f/D是透镜的f数，由透镜本身的设计决定。

为了得到更小的聚焦，我们可以使用小f数的透镜。同样也可以通过减小R（较小的透镜或者在透镜方面加孔阑）或增大s1来实现。但是采取其中的任何一种方式，都会限制透镜收集的光的总量。例如，如果我们把R减小一倍或者把s1增大一倍，那么透镜收集到的光的量将相应减小为原来的1/4。因此需要根据具体应用平衡选择。

激光元器件不同于传统光学的特点是：光学材料特殊，镜片表面高光洁度，光学膜系精准，激光损伤阈值高。 由于激光的种类繁多，光谱覆盖越来越广，功率越来越高，因此对于光学元件器件的指标要求也非常严格。鞍山激埃特光电拥有全面的精密制造和检测设备，如单点金刚石车床，CNC数控抛光机，高校冷凝泵镀膜机，数字式中心偏检测仪，干涉仪，激光真空热度仪，椭偏仪，分光光度仪等设备。

鞍山激埃特的光学工程师和质量管理团队为客户精心制造适合于高质量激光设备的激光光学元器件http：www.giaitech.com.cn